Hermite normal form
In linear algebra, the Hermite normal form is an analogue of reduced echelon form for matrices over the integers Z.
Contents |
Nonsingular square matrices
A nonsingular square matrix M = (mij) with integer entries is in Hermite normal form (HNF) if
- M is upper triangular,[1]
- its diagonal entries, mii, are positive,
- for j > i, mii > mij ≥ 0, i.e. in a given row, the entries to the right of the diagonal are less than the diagonal, and at least zero.
Example
The matrix
is in HNF.
General matrices
More generally, an m×n matrix with integer entries is in (HNF) if there exists
- r with 0 ≤ r ≤ n,
- a strictly increasing function f: [r + 1, n] → [1, m],
such that the first r columns of M are zero, and for r + 1 ≤ j ≤ n
- mf(j)j > 0,
- mij = 0 when i > f(j),
- mf(j)j > mf(j)k ≥ 0 when k > j.
Example
Here we have r=2; f(3)=1, f(4)=3, f(5)=4, f(6)=5. (f(j) gives the row of the lowest nonzero entry in column j.)
Uniqueness of the Hermite normal form
Given any m×n matrix M with integer entries, there is a unique m×n matrix H, in HNF, with integer entries such that
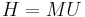 with U ∈ GLn(Z) (i.e. U is unimodular).
with U ∈ GLn(Z) (i.e. U is unimodular).
The matrix formed by the nonzero columns of H is called the Hermite normal form of M.
See also
Notes
- ^ Some authors prefer using lower triangular matrices; suitable adjustments must be made to the rest of the definition
References
- Section 2.4.2 of Cohen, Henri (1993), A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics, 138, Berlin, New York: Springer-Verlag, ISBN 978-3-540-55640-4, MR1228206

